Electromagnetic Acoustic Transduction (EMAT) is a method for applying mechanical signals to a test specimen. EMAT is receiving a lot of industry attention within the Nondestructive test field due multiple potential benefits such as its non-contact nature. One of the single biggest disadvantages of such a system pertain to low transduction efficiency, that is the level of energy required to generate amplitude comparable signals within a test specimen are far higher than other competing transduction methods such as piezo electric transduction, furthermore the transduction efficiency drops linearly (within limits) with lift-off. Using a fairly standard EMAT system a liftoff of just 2mm incurs a substantial drop in received signal of over 8db. Many EMAT systems are mobile crawling units designed to travel along a test specimen and the time implications of extensive averaging make the technique un-economical. With the use of carefully selected post signal processing the signal to noise ratio of an EMAT system maybe improved allowing for the identification of smaller defects, lower number of averages resulting in a faster unit travel speed and greater lift of distances. This report shows that the use of post signal processing methods such as Savitzky-Golay Filtering and Singular Spectrum Analysis enhance the lift of capabilities of EMAT systems without the need for continuous
Contents
Scope as defined by background research
Mechanical Design Work – Test Assembly Rig
Equipment Assembly and Data Collection
SPECTRUM file import and initial processing
FIR Zero Offset Bandpass Filter
Non-destructive testing (NDT) within the Oil and Gas sector has been in mainstream use for several decades with the purpose of providing information regarding the condition of a test specimen (pipe, tank etc). Ultrasonic testing equipment such as the Wavemaker™ product range developed by Guided Ultrasonics Ltd is able to identify and accurately locate internal and external defects caused by damage and corrosion within a section of pipeline that would otherwise be undetectable to visual inspection. Farley [1] notes that the value of NDT comes from the avoidance of the costs associated with plant downtime and from the mitigation of potential catastrophes, a major reason for growth within this industry is the life extension of an ageing infrastructure as a result of passing NDT. Frost and Sullivan [2] suggest that by 2017 the ultrasonic test equipment market will have an earned revenue of $585.7 million per year giving good incentive for companies to develop new and existing technologies to solve specific NDT problems.
In recent years, Electromagnetic Acoustic Transduction (EMAT) as a means to send and receive signals within a ferromagnetic material has grown in popularity. De facto transduction methods of NDT often make use of piezo transducers (PZT) which rely heavily upon surface contact between the transducer and the material under test, and as a consequence insulating materials and coatings must be removed prior to test. In contrast, Electromagnetic transducers do not need to be in physical contact with the material being inspected making industrial application more economical. Ashigwuike [3] notes that the major disadvantage of EMAT pertains to the low transduction efficiency which in turn results in a very low received signal amplitude and generally poor signal to noise ratio (SNR). The SNR of a time of flight (TOF) system limits both the size of the defect which can be detected and the distance that the equipment is able to scan.
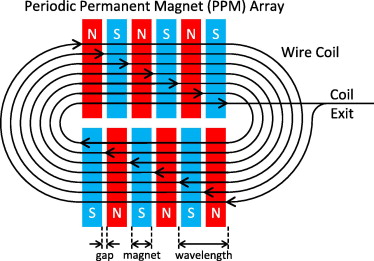
Figure 1 EMAT PPM Arrangement [4]
EMAT transducers comprise of a magnet stack and AC coil (see fig 1). The magnet stack provides a static bias magnetic field while the AC current in the coil interacts with the bias field to create strain within the test specimen. The mechanical strain in the test piece creates an ultrasonic wave which travels within the structure ‘guided’ by the material boundaries. When the wave encounters artefacts with a dissimilar mechanical impedance (defects, holes, end of test piece etc.) part of the original transmission is reflected. This reflected wave is received and converted into an electrical current using a similar but opposite mechanism to transmission. The very low voltage created by the current within the receiver coil is amplified using a special low noise amplifier and then sampled by a high-speed ADC within dedicated hardware to give positional and physical information regarding the source of reflection. Petcher et al. [5] shows that the strength of the transmitted and received signal is proportional to the strength of the bias magnetic field. The bias field strength is heavily dependent upon transducer lift off (gap between pipe surface and transducer), such a lift of maybe caused by pipe coatings such as thermal insulation or corrosion protection. It is clear to see that a reduction in signal strength will further decrease an already poor SNR.
Traditional signal processing techniques such as analogue filtering and averaging have been used to reduce signal noise. However, in the case of averaging it may be noted that averaging data N times reduces noise by a factor of
√N
. As an example; If the sample time is 500ms two averages would reduce noise by a factor of approximately 1.4 with a total sample time of 1S. A noise reduction of factor 10 would require approximately 128 averages, increasing total sample time to over 1 minute. This would be unacceptable for many mobile applications. Furthermore, averaging only works when the noise is random by nature. Physical methods of increasing SNR may include larger magnets, more powerful transmit electronics or more complex receiver circuitry all of which offer disadvantages in the form of efficiency, space and cost. It is therefore of great advantage to post process data sets using mathematical techniques to reduce noise and therefore increase SNR.
Signal processing is the application of mathematical and or statistically based algorithms implemented to extract useful information from a signal with noise – where noise may be defined as all signal and or frequency content which is not of interest. In recent years, the level of processing power available even in relatively standard laptop computers has facilitated the fast use of very complex signal processing algorithms. Many thousands of digital signal processing techniques have been developed, the suitability of each to perform a specific task requires careful evaluation and testing. Hassanpur [6] notes that a main concern regarding the development of such techniques is that the original data should not be deformed by the algorithm, the goal is to attenuate noise while maintaining the structure of the original signal, this should in the case of TOF measurement include shape, frequency and phase.
This project aims to implement and evaluate several signal post processing techniques using MATLAB with the intent of increasing the lift off potential of an EMAT based NDT probe by increasing the SNR of collected data. The transmitted and received signal strength of such a system is directly related to the lift off (distance from test specimen surface to probe), increasing the SNR of the collected data through post processing adds no time to the actual collection process and will allow useful data to be extracted from the low signal-noise data. This will allow items to be inspected which have thicker coatings (paint, insulation etc) and would have the potential of detecting defects which are currently not detectable using a simple system with poor SNR.
There are several project objectives, the completion of which will enable the main project aim to be met:
The project is to be completed at the premises of Guided Ultrasonics Ltd. where test equipment and lab space is available. The initial stages of this project are mostly hardware based requiring that a suitable test setup be constructed so that accurate data maybe collected and stored ready for later MATLAB based signal processing experiments. This section of the report intends to outline the planned activities for each of the main project milestones.
Figure 2- Intended workflow with main milestones noted
In order for the project to be completed within the specified time frame several project planning techniques have been used. These include a WBS (work breakdown structure appendix B), TBS (task breakdown structure appendix C) and Gantt chart (appendix D). These are available within the appendix section of this report and will naturally change as the project progresses towards completion.
Background research was conducted into various signal processing methods used to de-noise signals. As a result of this research three main areas were selected for further research and eventual development. The three areas which ultimately form the scope for this project are:
A brief summary of the research conducted into each area is as follows:
Milivojević [7] states that there are two major groupings of digital filter, finite impulse response (FIR) and infinite impulse response filters (IIR). Each grouping has the following characteristics:
FIR
IIR
Due to potential stability issues which could be incurred with IIR filtering the author chose to dedicate further research into FIR filtering. Milivojević [7] later states that due to their higher orders FIR filters should only be used when linear phase characteristics are important. Because the data which will be collected within this project is time of flight data, where timings are made based upon signal phase it is incredibly important that phase data be maintained when any form of filtering is applied. The main filter types which will be used within this project are High pass – where frequencies below a cut off are attenuated, Band pass – where frequencies outside of two bands (upper and lower) are attenuated and Low pass filtering – where frequencies below a above a cut off frequency are attenuated. Furthermore, due to the linear phase characteristics of an FIR filter any time delays incurred through its use may be accounted for.
Ferenc-Emil et al [8] state that many FIR filter algorithms are implemented using a series of delays, multipliers and adders in order to achieve a specific filter response which suggests that one potential result of FIR digital filtering maybe the introduction of some form of overall time delay. Further study into the area yielded several MATLAB functions which are designed to easily implement zero offset digital filters which will be explored during the code implementation section of this project.
The Savitzky-Golay [9] Filter implementation was presented in 1964 by Marcel J. E. Golay and Abraham Savitzky as a method to smooth noisy data by averaging adjacent data points with a best fit low order polynomial using the least squares method. For their application, the common method of using running averages was not good enough for the extraction of spectral peaks. One of the goals of this project is to increase the SNR of a signal in place of the NDT convention of using running averages. Dagman and Kavalcioglu [10] show that the application S-G filtering is very simple whilst maintaining characteristics such as maximum and minimum peaks.
The S-G filtering technique appears to be a good solution to the smoothing of low SNR data, especially if the noise is made up of a high frequency content. MATLAB provides comprehensive information regarding the S-G filter together with several easy to apply functions which will make performance evaluation of the technique within this project straightforward. Further Gander and Matt [11] stipulate that a main advantage of the Savitzky-Golay filter is its speed as filter parameters only need to be evaluated once, this potentially facilitates real time implementation in hardware such as DSP and FPGA’s.
Golyandina and Zhigljavsky [12] describe Singular Spectrum Analysis (SSA) as being a technique of time series analysis and forecasting which combines elements of classical time series analysis, multivariate statistics, multivariate geometry, dynamical systems and signal processing. Where SSA aims to decompose an original time series into a sum of a small number of interpretable components such as trends, oscillatory components and noise. The techniques history begins with Broom-head and King (1986a, 1986b) where they show that singular value decomposition is to able to reduce noise. Myung [13] breaks the application of SSA down into four steps;
The ground up development of an SSA techniques is beyond the scope of this project however a simplified explanation of the steps given by Myung are as follows:
Embedding
Embedding is the process where the original time series data is mapped to a series of windowed, lagged vectors. The output of this stage is the trajectory matrix.
Singular Value Decomposition
SVD is applied to the trajectory matrix in order to perform decomposition of the trajectory matrices into a number of time series components, the result of SVD application to trajectory matrices are so called eigentriples. SVD is used minimise a data set by removing elements which do not largely contribute to reconstruction, instead an optimal approximation of the trajectory matrix is formed.
Grouping and diagonal averaging
Grouping is the first reconstruction step and is named due to the eigentriple grouping which takes place, where groups of eigentriples are used to reconstruct principal components with original time units. Components with large singular values are taken to be signal while the rest is considered to be noise. Some methods of SSA use more elaborate statistical measures to determine what a ‘large singular value’ is, further the wanted signal may not actually be the eigentriple with the largest single value. Seekings et al [14] presents an excellent discussion regarding the statistical grouping by using the Kurtosis value of each time series component.
The final step of SSA is the reconstruction of eigen triples into a new time series using diagonal averaging, which is also referred to as Hankelisation. Hankelisation by diagonal averaging is applied to each eigentriple inverting the eigentriple back into a set time series components which sum to equal the original time series data.
Hassani [15] lists SSA as being a very versatile tool which has a broad range of applications some of which include: Finding trends in data, signal smoothing, simultaneous extraction of cycles with small and large periods and extraction of periodicals with varying amplitudes. Due to this broad array of applications the author believed that it was likely that SSA could be applied to the subject topic.
The evaluation of project output will be broken into two parts
In order for performance evaluation to take place real data must be collected according to a consistent procedure (so as not to introduce measurement error between files). Data will be collected using a Wavemaker G4mini instrument, a proprietary (to Guided Ultrasonics Ltd.) low noise instrumentation amplifier, high current pulse amplifier and EMAT coils. The coils will be placed upon the test specimen initially with zero lift off.
Figure 3 shows a simplified equipment connection diagram and an example of a 6-cycle pulse which will be transmitted by the high current pulse amplifier and EMAT coil at a frequency determined by experimentation to ensure that a dominant SH0 (Shear Horizontal zero mode) wave is transmitted within the test specimen. The excitation frequency required to generate a dominant SH0 wave is material thickness dependent. The receiver coil and amplifier will receive the transmitted signal where the G4mini instrument will further amplify and sample the signal at 2.5Mhz over 2000 data points. The results will form a benchmark data set with a relatively good SNR. A collection will then be performed without any transmitted signal, this test aims to record the baseline noise over 2000 data points for later processing/evaluation. This test will be performed again with various lift off distances from coil and test specimen as per Table 1, the data will be stored for later testing with the (to be developed) signal processing algorithms.
Table 1 – Proposed Data collection schedule
| Test No. | Test Description |
| 1 | Zero Lift 0 Averages– Baseline |
| 2 | Zero Lift 64 Averages – High SNR |
| 3 | 1mm Lift 0 Averages |
| 4 | 2mm Lift 0 Averages |
| 5 | 3mm Lift 0 Averages |
| 6 | 4mm Lift 0 Averages |
SH0 transmission has been selected because it is a non-dispersive wave mode. Lowe et al. [16] describe a non-dispersive wave mode as being a traveling wave with a constant velocity regardless of frequency so that the signal shape and amplitude are retained as it travels. For these experiments, non-dispersion will mean that the received signal will match closely in shape with that of the transmitted signal which may allow use of some shape matching algorithms during code development. SH0 (because of its non-dispersive behaviour) occurs at all frequencies, higher order modes (SH1, SH2 etc) are frequency dependent. To ensure that SH0 is the dominant transmitted wave mode experimentation using different frequencies must take place during the data collection process.
Solidworks 3D modelling software was used to design a test assembly to fulfil the following simple specification:
Figure 4 – Test assembly rig as designed using Solidworks 3D Modelling software
Figure 4 shows the test assembly rig as modelled. All design specification points have been achieved. Simple lift-off adjustment is accomplished with the use of 1mm thick PTFE shims which will be placed under each module to achieve a sensor lift of distance of between 0 and 4mm. Unfortunately, detailed images of module electronics, magnet stack arrangement and coils may not be given – they are propriety to Guided Ultrasonics. However detailed drawings of module enclosures and locating frame are given in appendix A.
The transducer test rig as modelled in Figure 4 was manufactured using a mix of selective laser sintering (3D printing) for the electronics enclosures and aluminium laser cutting for the frame. The 1mm PTFE shim spacers were hand cut from PTFE sheet. The component parts were easily assembled before testing was initiated.
Data collection was conducted according to the procedure outlined in the previous Evaluation Method and Plan section of this report with additional files recorded as tabulated below. The test specimen pictured in Figure 6 is an 18” steel pipe with a wall thickness of 12mm.
A frequency of 170Khz was found by experiment to give the highest amplitude SH0 received signals. Table 2 gives the results of data collections which will be used within the signal processing section of this project.
Table 2 Data recorded using test assembly rig for later processing
| Test Number | File Name/Description | Recorded SNR (dB) |
| 1 | 0mm lift-170Khz-0AVG-44db-2000.tim | 25.68 |
| 2 | 0mm lift-170Khz-64AVG-44db-2000.tim | 28.30 |
| 3 | 0mm lift-NOISE-170Khz-64AVG-44db-2000.tim | 0 – Noise only |
| 4 | 1mm lift-170Khz-0AVG-44db-2000.tim | 21.00 |
| 5 | 2mm lift-170Khz-0AVG-44db-2000.tim | 18.05 |
| 6 | 3mm lift-170Khz-0AVG-44db-2000.tim | 8.44 |
| 7 | 3mm lift-170Khz-0AVG-56db-2000.tim | 8.44 |
| 8 | 4mm lift-170Khz-0AVG-44db-2000.tim | 5.61 |
| 9 | 4mm lift-170Khz-0AVG-56db-2000.tim | 5.29 |
| 10 | 4mm lift-170Khz-4AVG-56db-2000.tim | 9.92 |
| 11 | 4mm lift-170Khz-8AVG-56db-2000.tim | 13.26 |
| 12 | 4mm lift-170Khz-16AVG-56db-2000.tim | 16.16 |
| 13 | 4mm lift-170Khz-32AVG-56db-2000.tim | 16.76 |
| 14 | 4mm lift-170Khz-64AVG-56db-2000.tim | 20.10 |
Code development has been accomplished with the exclusive use of MATLAB. MATLAB is a high-performance maths oriented coding environment where code maybe quickly written and tested. Code was created to implement each of the functions listed in the flowchart shown within the work breakdown structure (Appendix B). Initially code was written as a MATLAB script, however the author found it more practical to convert each written script to a MATLAB function which could then be called by a simple main script for testing and then more easily incorporated into a graphical user interface. This section intends to give an overview of each of the developed MATLAB functions with brief testing and discussion of any technical problems. Full code for each function will be given in the appendix of this report.
Data was collected using the apparatus setup as shown in Figure 6. Data is initially stored as a .tim file which is a text based file output from SPECTRUM™. The .tim file contains amplitude data for each sampled point, time step information, time offset information (start of file is not the centre of transmit pulse), number of points recorded and the units for time and amplitude. An example of a .tim file can be seen in Figure 7.
The file must be imported into MATLAB in the form of an array for later processing. File import was accomplished by adaptation and use of pre-existing function ‘loadSpectrumHist’ (appendix CD-A). A time vector is created by multiplying the total length of the output file by the time step between each sample as can be seen in Code 1.
The amplitude output data from the loadSpectrumHist function may now be plotted against the time vector. Code 2 gives a sample of the code used to plot graphs, it is repeated many times throughout code and GUI development.
plot(time_vec,spectrumhist, ‘k’);
xlabel(‘Time (S)’);
ylabel(‘Amplitude’);
legend(‘Raw Time Data’);
axis([0 inf -0.02 0.02]);
grid on;
Figure 8 shows the output of the code shown in Code 2. Note the presence of a time offset at the beginning of the plot. This section contains no useful information as the user is looking at reflections after the initial (clipped) transmit pulse. Classically users of NDT software expect the data shown at time = 0 to be at the centre of the excitation pulse. To apply appropriate time offset the function RT_Signal_cutting.m (appendix CD-B) was written and is used during file import.
Further some of the later signal processing methods may rely upon the signal being centred about 0V. Analogue amplification can also amplify DC offsets which may be caused due to amplifier overload. In order to strip any DC offset from the data a simple zero offset high pass filter was constructed using the MATLAB filtfilt function which corrects any time offset created as an effect of the filter phase response. This filter attenuates frequencies below 10Khz with a cuttoff frequency of 1Khz at -60dB. Code 3 gives example application of zero offset high pass filter.
The imported data amplitude varies as a result of lift of and received signal amplitude, however the initial transmission pulse shown as a clipped square wave in Figure 8 is a result of the analogue collection amplifiers input protection diodes. This voltage is very consistent. To aid in the visual inspection of SNR for different data sets a simple normalisation function was written (RT_Signal_normalise.m appendix CD-C) The function adds a multiplication factor to the entire signal (after transmission) so that the first received pulse amplitude matches that of the clipped data.
Figure 9 shows the imported .tim file post high pass filtering, time offset and normalisation to clip amplitude. This data is stored in an array for use by later signal processing functions.
FIR Zero phase bandpass filtering is performed in order to attenuate out of band frequency content. The transmitted signal frequency is 170Khz and forms the centre frequency of the bandpass filter function RT_BANDPASS.m shown in appendix CD-D. The MATLAB designfilt function is used in order to define or adjust the filter coefficients which include setting of the pass, stop and centre frequencies as well as the stop band attenuation and pass band ripple. These coefficients are set externally from the function so that they may easily be altered by the user.
The bandpass coefficients which are called by the function are by default as follows:
Figure 10 shows the visualised filter using coefficients defined in Code 4, Figure 11 shows data pre/ post bandpass filtering.
Initially filter code design was accomplished by using standard FIR filter options however due to the nonlinear phase response of the FIR filter a group delay occurs where different frequencies are delayed by different amounts. Not only does this result in an overall time offset with respect to input data but it also distorts the signal.
The MATLAB filtfilt function filters the input data in the forward and reverse directions which effectively cancels the error created by the nonlinear phase response resulting in the original time offset being maintained as well as not distorting the filtered signal. A script was written with filter coefficients as listed in Table 3 to quickly demonstrate the effects of a filter delay, Figure 12 shows the Filter_Delay.m (appendix CD-E) output. It is clear to see that the filtfilt function works well and introduces no noticeable delay making it much more suited to the intended application one point to note is that because the filtfilt function effectively passes the data through a filter twice the filter order is doubled.
Table 3 Bandpass Filter default coefficients
| Centre Frequency | 170 Khz |
| Pass Bandwidth | 50 Khz |
| Stop Bandwidth | 200 Khz |
| Stop Band Atten. | 80 dB |
| Pass Band Ripple | 0.1 dB |
The Savitzky-Golay filter (least squares filter) operates to smooth data without adding time delay or signal distortion in the same way that a standard FIR filter would. The filter achieves smoothing by fitting a low order polynomial to a group of data points surrounding a ‘target’ data point using the least squares method. It operates in a similar manor to a moving average filter. Advantages of the S-G filter are speed and that the peak height/shape of waveforms is maintained. A Savitzky-Golay filter may be easily implemented using the MATLAB function sgolay. A function named RT_SG_SMOOTH.m has been created and may be seen within appendix CD-F. Figure 13 presents the output from such a filter as well as an FFT plot which shows the S-G filter effectively acting as a low pass filter for this data set which stands to reason as averaging between data points would attenuate the high dv/dt between points.
The singular spectrum analysis script used to create the function RT_MOD_SSA_Kurtosis.m (appendix CD-G) takes a one-dimensional time series data input and converts it into a number of windowed multi-dimensional trajectory matrices. In this instance, the trajectory matrix is non-square which requires the use of the MATLAB function hankel to be used. Within a hankel matrix the elements within the diagonal
i+j=const
are equal. Economic singular value decomposition (SVD) of the trajectory matrix into left singular vectors, singular values and right singular vectors (U S V) is completed using MATLAB function SVD. Zeros are removed (which do not contain information required to reconstruct the data series). Reconstruction occurs via eigentriple grouping
U*S*V
. At this point each reconstructed eigentriple is evaluated by kurtosis value measurement. If the kurtosis, a statistical measure which describes the distribution of data points about a mean or ‘peakedness’ value is smaller than a predefined threshold the eigen triple is considered to be unwanted and is set to zero. The kurtosis value for Gaussian white noise is close to 3. The reconstructed data matrix is then diagonally averaged to complete the SSA process.
Figure 14 Input data (Red) vs. SSA-Kurtosis threshold filtered data (Blue)
Figure 14 shows SSA filtered data. The SSA algorithm during initial testing gave a larger improvement in SNR than S-G and bandpass filtering.
The user interface (named Ampullae) operates and runs within MATLAB. The GUI intends to make data import using the windows file structure and iterative processing using the various covered techniques simple and fast. The user has the ability to apply one or all of the available signal processing functions in any combination, any number of times. This approach allows for a quick ‘trial by error’ approach to finding the best combination of functions to improve the SNR as much as possible.
The interactive GUIDE tool which is included within MATLAB was used to create the GUI. Ampullae is formed of several signal processing tools and also several sub graphical user interfaces aiming to aid the user.
Main Ampullae GUI
The main graphical user interface (code available in appendix CD-H) enables the user to import and open a .tim file using the windows file structure. Apply S-G smoothing, Bandpass filtering, signal normalisation, simple SSA (SSA without kurtosis thresholding), SSA with kurtosis threshold and SNR analysis in any order any number of times. Upon completion, the processed data may either be reset or exported to a .tim file. The SNR function RT_SNR.m (appendix CD-I) is called using the ‘Run SNR’ button and is a simple function which measures the peak to peak voltage of a good window and noisy window. The SNR is calculated using the following common formula and displayed below each time trace for quick signal comparison:
SNR=20*logSignal VRMSNoise VRMS
Sub GUI – Kurtosis Inspector
The Kurtosis Inspector tool (shown in Figure 16) is a complementary sub graphical user interface designed to make the estimation of kurtosis thresholding value simpler. The tool also allows the user to inspect the difference in kurtosis between wanted signal (normally higher) and noise before setting the main kurtosis threshold within the Ampullae screen. Code for the Kurtosis Inspector is given within appendix CD-J.
Sub GUI – Bandpass Setup
The Bandpass Setup tool (shown in Figure 17) is another complementary sub graphical user interface which makes setting the bandpass filter coefficients simpler for the user. The interface also allows the user to simulate and visualise the filter response with a single button click. Input variables are passed back to the Ampullae GUI through the use of global variables and set/get.appdata functions. Default bandpass filter coefficients are loaded when the ‘Load Spectrum File’ button is selected meaning that the user does not always have to enter the Bandpass setup tool to set values- these default values are ‘fetched’ by the Bandpass Setup tool by selecting the ‘Grab Default Settings’ button.
This section presents and gives discussion to the results obtained from initial data collection and from post processed original data using the functions outlined in the code development section of this report.
Table 2 lists the data sets which were collected for processing. Files 1,4,5,6,8 have been selected for evaluation due to their matching zero averages and gain. The signal processing techniques studied within this report were applied to the listed data files in Table 5 to assess the SNR improvement as a result of applying each function individually. The SNR tool introduced within the code design section of this report (appendix CD-I) was used with window position as shown in Figure 18, the Kurtosis threshold was set to 3.4 and the bandpass filter coefficients are default values as listed in Table 3.
Table 4 File ID, File name and description to be processed
| File ID | File Name | Description |
| 1 | 0mm lift-170Khz-0AVG-44db-2000.tim | 0mm lift, amplifier gain 44dB, transmit at 170Khz |
| 4 | 1mm lift-170Khz-0AVG-44db-2000.tim | 1mm lift, amplifier gain 44dB, transmit at 170Khz |
| 5 | 2mm lift-170Khz-0AVG-44db-2000.tim | 2mm lift, amplifier gain 44dB, transmit at 170Khz |
| 6 | 3mm lift-170Khz-0AVG-44db-2000.tim | 3mm lift, amplifier gain 44dB, transmit at 170Khz |
| 8 | 4mm lift-170Khz-0AVG-44db-2000.tim | 4mm lift, amplifier gain 44dB, transmit at 170Khz |
It was found that the noise amplitude remained constant regardless of lift-off distance 0-4mm. Graph 1 shows that the reduction in SNR was fairly linear with lift off. This was unexpected as the author believed that small amounts of lift off would yield little signal loss whilst moderate lift off distance would have a much larger effect. This linear reduction in SNR reduction is likely due to the linear reduction in magnetic field intensity with respect to the test specimen. Further testing with different specimen materials may allow for the prediction of SNR with regard to a known lift off distance.
Table 5 Data files, SNR original vs. processed for different processing functions
| File ID | Original SNR (dB) | S-G Filtering (dB) | Bandpass Filter (dB) | SSA Kurtosis (dB) |
| 1 | 25.55 | 29.74 | 28.85 | 28.12 |
| 4 | 21.61 | 27.30 | 28.16 | 29.08 |
| 5 | 17.43 | 25.87 | 27.21 | 28.2 |
| 6 | 8.44 | 15.13 | 16.25 |
∞ |
| 8 | 5.61 | 11.31 | 15.57 | ∞ |
Each signal processing technique returned a significant increase in SNR. It is interesting to note that the SSA functions worked better on slightly noisy data. This was caused as a result of the wanted signal being attenuated in files with an already high SNR, for files with a lower starting SNR the wanted signal was not noticeably attenuated. For files with a very low SNR (3 and 4mm lift) the Kurtosis thresholding of the SSA filer resulted in many data points being classified as noise and set to zero giving a false SNR of
∞
. The S-G and Bandpass Filter gave a consistent increase in SNR while the SSA filter when able to be applied outperformed both.
Through experimentation it was found that a combination of the three filtering functions applied in the order: Bandpass, SSA, S-G resulted in the highest increase in SNR. Table 6 shows that for lift off distances of 2mm and less the SNR is increased for all files to over 30dB. It should be noted that the 2mm lift combination processed signal shown in Figure 19 shows a significantly higher (4.44dB) signal to noise than that of a zero-lift signal. Graph 2 shows that the SNR increased as the input SNR decreased as there is more ‘noise’ signal for the filters to work on however the 4mm lift off data does not follow this trend giving a lower SNR improvement. This is perhaps due to the noise energy approaching that of the signal making noise separation and attenuation a more complex task for lift off distances of 4mm and greater.
Table 6 SNR improvement resulting from the application of a combination of functions
| File ID | Original SNR dB | Combination Filtered SNR dB | Delta SNR Increase dB |
| 1 | 25.55 | 31.72 | 6.17 |
| 4 | 21.61 | 30.73 | 9.11 |
| 5 | 17.43 | 30.12 | 12.6 |
| 6 | 8.44 | 23.31 | 14.87 |
| 8 | 5.61 | 13.9 | 8.29 |
To assess the effectiveness of collection averaging where multiple data collections are performed and averaged in order to reduce the fairly random (frequency spectrum) noise and to give reference to the extra time required to complete a large number of averages Graph 3 was plotted. The result is as expected, a linear increase in SNR is accomplished by a square increase in number of averages.
The graph shows quite clearly that the relationship between number of averages/SNR improvement and time is not linear. Very quickly squaring the number of averages to double the SNR becomes time inefficient.
Graph 3 SNR improvement vs. no. of averages with total collection time vs. no. averages
The goals defined at the beginning of this project have been achieved. Several signal processing techniques have been explored and a simple to use graphical user interface has been realised allowing straight forward application of aforementioned techniques. Figure 19 ultimately shows the true outcome from this project in that with the application of project MATLAB functions data collected using electromagnetic transduction with a substantial lift off distance may be post processed to achieve a signal to noise ratio which meets or even exceeds that of similar data with a zero lift off distance. Within the NDT field traditional signal processing methods which aim to reduce signal noise are usually limited to the application of data averaging and bandpass filtering. This project shows, with evidence that these traditional methods maybe improved upon with the post application of methods such as Singular Spectrum Analysis. The outcome of this is twofold; for applications with minimal lift off a lower powered system may be deployed, or for higher powered systems the useful range of operation pertaining to the lift off distance is increased.
As with many signal processing challenges there is not a ‘one size fits all’ solution. While this report shows that SSA yields good results for files with a moderately poor SNR of between 15 and 20 dB (increasing SNR by over 10 dB in some cases) it does not work as well with very high SNR data or very low SNR data (sub 10 dB). In these cases, the statistical threshold values must be carefully considered and other filtering methods applied pre SSA. A system with pattern recognition or machine learning capabilities which is able to adaptively apply a broad range of methods in order to achieve large improvements to SNR should be the ultimate evolution of this project.
Project output;
| [1] | M. Farley, “40 years of progress in NDT – History as a guide to the future,” API conference proceedings, no. 0094-243X, p. 5, 2014. |
| [2] | Frost & Sullivan, “Replacement of Radiography by Phased Array Ultrasonic Testing Drives Global Ultrasonic NDT Equipment Market,” PR Newswire US, p. 1, 19 11 2013. |
| [3] | E. C. Ashigwuike, “Coupled Finite Element Modelling and Transduction Analysis of a Novel EMAT Configuration Operating on Pipe Steel Materials,” 2014. |
| [4] | B. D. Petcher, “Shear horizontaL(SH) ultrasound wave propagation around smooth corners,” Ultrasonics, vol. 54, no. 4, p. 998, 2013. |
| [5] | D. Petcher, “Weld defect detection using PPM EMAT generated shear,” NDT&E International, vol. 74, p. 51, 2015. |
| [6] | H. Hassanour, “A time-frequency approach for noise reduction,” Digital Signal Processing, vol. 18, no. 5, p. 1, 2007. |
| [7] | Z. Milivojević, Digital Filter Design, MikroElektronika, 2009. |
| [8] | G.-S. Z. Mózes Ferenc-Emil, “IMPLEMENTATION OF DIGITAL FILTERS IN FPGA,” Scientific Bulletin of the Petru Maior University of Targu Mures, vol. 8, no. 2, p. 94, 2011. |
| [9] | M. J. E. G. Abraham. Savitzky, “Smoothing and Differentiation of Data by Simplified Least Squares Procedures.,” Analytical Chemistry, vol. 36, no. 8, p. 1627, 1964. |
| [10] | C. K. ˘. Berk DAGMAN, “FILTERING MATERNAL AND FETAL ELECTROCARDIOGRAM (ECG) SIGNALS USING SAVITZKY-GOLAY AND ADAPTIVE LEAST MEAN SQUARE (LMS) CANCELLATION TECHNIQUE,” Bulletin of the Transilvania University of Bra¸sov, vol. 9, no. 8, pp. 109-124, 2016. |
| [11] | U. v. M. W. Gander, Solving Problems in Scientfic Computing Using Maple and Matlab, Berlin Heidelberg: Springer-Verlag, 1993, pp. 121-139. |
| [12] | A. Z. Nina Golyandina, Singular Spectrum Analysis for Time Series, Berlin Heidelberg: Springer-Verlag , 2013. |
| [13] | N. K. Myung, Singular Spectrum Analysis, Los Angeles : University of California, 2009. |
| [14] | M. H.-K. A. A. P. L. M. H. John Potter, “Denoising Dolphin Click Series in the Presence of Tonals, using Singular Spectrum Analysis and Higher Order Statistics,” in OCEANS 2006 – Asia Pacific., Asia Pacific, 2006. |
| [15] | H. Hassani, “Singular Spectrum Analysis: Methodology and Comparison,” Journal of Data Science, vol. 5, pp. 239-257, 2007. |
| [16] | A. C. Lowe, “Defect detection in pipes using guided waves,” Ultrasonics, vol. 36, no. 1-5, p. 149, 1998. |
| [17] | F. M. Last Name, Book Title, City Name: Publisher Name, Year. |
Figures
Figure 20 Original data files 1,4,5,6,8 with zero processing
Figure 21 Original Data files post normalise and offset
Figure 22 Fully combination processed data files
The appendix section of this report has been broken into two parts. The first appendix part is a traditional appendix with the following items
| Appendix ID | Description |
| A | 3D Cad drawings for test rig |
| B | Project Work Breakdown Structure |
| C | Project Task Break Down Structure |
| D | Final Project Gantt Chart |
The second section of the appendix comprises all of the MATLAB code generated as a result of this project including original data files which can be processed to show code operating principals. The Author advises that all files be placed into a folder which may be added to the current MATLAB path. The data files may remain in a separate folder however for expedience it is recommended that this folder also be added to the same location as other files. It is recommended that the code be initiated by running Ampullae_GUI.m
| Appendix ID | Description |
| CD-A to CD-K | Functions adapted or developed for project |
| CD-L | Functions not adapted or written by author but used during code development |
| CD-M | Original example files |
Appendix A – CAD DRAWINGS
Appendix A – CAD DRAWINGS
![C:UsersAdminAppDataLocalMicrosoftWindowsINetCacheContent.WordWork Breakdown Structure].jpg](https://images.ukdissertations.com/18/0025612.032.jpg)
Appendix B – WBS
Appendix C – TBS
Appendix D – Gantt Chart
You have to be 100% sure of the quality of your product to give a money-back guarantee. This describes us perfectly. Make sure that this guarantee is totally transparent.
Read moreEach paper is composed from scratch, according to your instructions. It is then checked by our plagiarism-detection software. There is no gap where plagiarism could squeeze in.
Read moreThanks to our free revisions, there is no way for you to be unsatisfied. We will work on your paper until you are completely happy with the result.
Read moreYour email is safe, as we store it according to international data protection rules. Your bank details are secure, as we use only reliable payment systems.
Read moreBy sending us your money, you buy the service we provide. Check out our terms and conditions if you prefer business talks to be laid out in official language.
Read more